Project Proposal: Skeleton-based Altas Construction for Meshes
Background
Atlas parameterization is a powerful tool: Given a 3D mesh, we create a rectangular grid, or atlas, which covers the mesh with minimal deformation between neighbor cells. Atlases have many applications in CAD/CAM, geometric modeling, computer graphics (texture atlases), and shape matching.
Creating high-quality atlases is very challenging. In particular, it is hard to create an atlas where the cell edges are somehow aligned with the structure of the object's features. In the image below, for example, the texture atlas is nicely aligned with the horizontal upper-edge of the seat. However, the atlas is unnaturally skewed along the bottom front-part of the seat.

Skeleton-based atlases
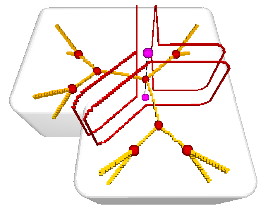
Curve skeletons are powerful descriptors for 3D shapes. They are thin structures locally centered with respect to an input shape, and capture the part-whole shape structure. More interestingly, curve skeleton points can be mapped to input surface points via geodesic curves. The image below shows a L-shaped box with its curve skeleton in orange. Several points are selected on the curve skeleton. These map back to three geodesics on the shape's surface (red curves).
Goal
Recently, we have perfected a surface-and-curve skeleton extractor from polygonal meshes. This method can extract skeletons and compute corresponding geodesic mappings in seconds for large meshes. The image below shows several such geodesics constructed from the skeleton of a cow model. Note that they are locally
- parallel with each other
- following the maximal surface curvature

In this project, we want to study how use 3D skeletons to create atlas-like parameterization of complex meshes, which are also naturally aligned with mesh features like high curvature areas. Several algorithmic and implementation challenges exist:
- what are the exact properties of skeleton geodesics? How do they relate to the surface curvature? When do they intersect (if ever)?
- how to create a uniformly-spaced set of geodesics covering an entire surface?
- how to create a similar set of parallel curves, orthogonal to the geodesics?
- how to combine the two sets to form a surface atlas (like the seat image, but better)
- how to implement all above efficiently using CUDA?
Requirements
The candidate should have the following skills:
- (very) good mastery of C/C++
- familiarity with CUDA programming
- basic knowledge of OpenGL
- familiarity with computational geometry
Contact
If you are interested in this project, contact Alex Telea. This project is a cooperation with dr. Andrei Jalba, Univ. of Eindhoven.
References
First, check the project pages accessible via links in the above text. Next, have a look at the following papers:
- Texture Atlas Generation for Inconsistent Meshes and Point Sets (P. Degener, R. Klein, Proc. IEEE SMA, 2007, 156-168)
- Computing Multiscale Curve and Surface Skeletons Using a Global Importance Measure (D. Reniers, J. van Wijk, A. Telea, IEEE TVCG, 2007)
- Hierarchical Part-type Segmentation using Voxel-based Curve Skeletons
(D. Reniers, A. Telea, The Visual Computer, 2008)
- Part-type Segmentation of Articulated Voxel-Shapes using the Junction Rule
(D. Reniers, A. Telea, Computer Graphics Forum (Proc. Pacific Graphics), 2008)