3D Shape Segmentation
Shape segmentation refers to the process of partitioning a given shape into typically non-overlapping, compact segments whose union is the original shape. Segmentation has many applications in computer animation, shape matching, shape compression and searching, and computer vision.
Two main types of segmentation methods can be distinguished:
- part-based segmentation divides a shape into its perceptually natural parts, like the legs, hands, head, and torso of a human body
- patch-based segmentation divides a shape into quasi-flat patches separated by creases or edges
Part-based segmentation is mostly used for natural, smooth, shapes. Patch-based segmentation is mainly effective for artificial shapes with a polyhedral structure.
Skeletons and segmentation
Interestingly, 3D skeletons can be readily used to produce shape segmentations which are natural, robust, and have a multiscale property, as follows
- surface skeletons produce patch-based segmentations
- curve skeletons produce part-based segmentations
Part-based segmentation
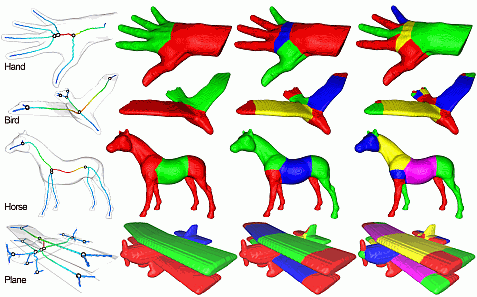
Given a 3D curve skeleton, we detect its junction points using a robust method we call the junction rule. Next, we map each skeleton part between junctions, or branch, to the shape's surface using the feature transform. Given the way we compute curve skeletons, the separation boundaries between parts will be smooth piecewise-geodesic curves, which yields a very natural shape partition, as shown below.
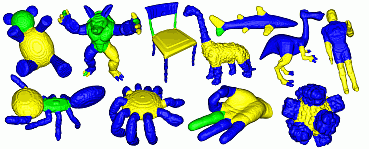
Pose invariance
A desirable property of our method is that segmentations are pose invariant. That is, given an articulated object, its different instances, or poses, will be segmented in effectively the same way. This is shown below on several shapes from the McGill shape benchmark.

Patch-based segmentation
The curve terminations of the sheets of a 3D surface skeleton correspond to curvature maxima, or edges, of its shape. Shape curvature minima, or creases correspond to terminations of the sheets of the skeleton of the shape's background. The feature points of the skeleton cover the entire shape. If we slightly simplify a skeleton, this will remove feature points precisely along these edges and creases, allowing us to detect them. Having the edges and creases, we can now segment the shape into quasi-planar patches, using a flood-fill algorithm variation.
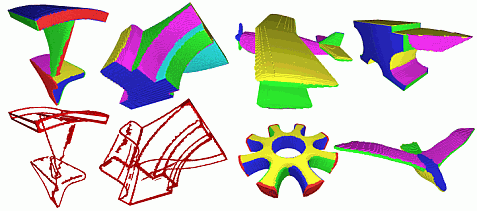
Noise resistance
Many methods exist that use curvature to segment shapes. In contrast to some of these, our method is extremely robust to noisy and poorly discretized shapes. The reason is the high stability to noise of the simplified skeleton.
The image below shows the skeletons (top) and segmentations (bottom) of two noisy, poorly voxelized, shapes. Note how the segments nicely follow the actual shape edges.
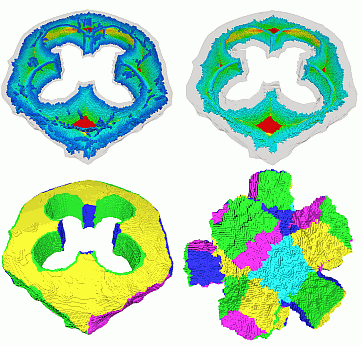
Smooth shape segmentation
Curvature-based methods also have problems when given very smooth, edge-less, objects. Although edges can be computed using scale-space methods that involve high-support filters, this will yield inexact, blurred, edge positions, thus bad segmentations. Our skeleton-based segmentation does not have this problem, since skeletons always point to the centers of blunt edges.
The image below shows the detected edges (left) and segmentations (right) of two smooth shapes. The segments are nicely separated at the precise locations of the curvature maxima.
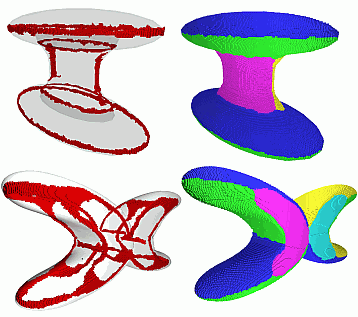
Hierarchical segmentation
Since our 3D curve skeletons are multiscale, we can use this property to produce multiscale part segmentations. For genus 0 shapes, the curve skeleton is a tree with the skeleton importance decreasing from the root to its leafs. Different methods are possible to construct a segment hierarchy from the multiscale skeleton, see our paper for details.
The images below shows several hierarchical segmentation levels for different shapes.
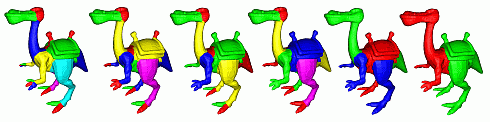
Segmenting 3D skeletons
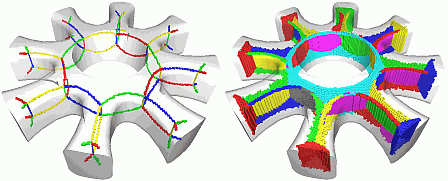
For some applications, it is useful to be able to treat the different manifolds of a 3D skeleton, and branches of a 3D curve skeleton, separately. For this, we need to segment the actual skeleton. For this, we compute the so-called ''Y-network' containing all curves where three or more skeletal manifolds intersect. We find these curves easily since their points have three or more distinct feature points on the shape. Next, we use flood-fill to segment the skeleton, given that it is voxel-thick and thus clearly partitioned by our Y-network. For details, see our paper.
The image below shows the Y-network (top0 and segmented surface skeletons (bottom) of several shapes. Note that the segmentation is robust even for noisy objects.

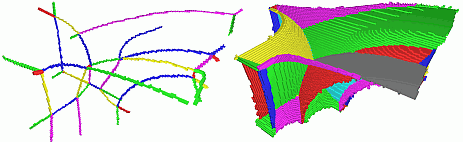
We can also apply our method to segment curve skeletons. The images below show the segmented curve skeletons (left) and surface skeletons (right) of two shapes from the INRIA 3D shape database. The original 3D meshes were voxelized prior to skeletonization and segmentation.
Software
The segmentation methods described here are implemented within our 3D skeletonization software.
