Kernel Density Estimation-based Edge Bundling
Edge bundling is a recent, increasingly promising, technique which generates graph layouts of limited clutter. Bundled layouts can be used to get insight into the coarse-scale structure of networks, geographical maps, and software systems.
For general graphs, many bundling methods have been proposed in the last few years. However, the following requirements are still challenging
- bundle graphs of tens..hundreds of thousands of edges efficiently (near-real-time)
- declutter graphs with many overlapping edges and nodes
- intuitively control the look and feel of the bundling (e.g. produce smooth or ramified bundles)
- easy implementation (no complex parameter settings or algorithms)
Kernel density estimation
We present here a method that complies well with the above requirements. The principle of our method is simple. Given an initial graph drawing
- convert the drawing to a density map using kernel density estimation (KDE)
- compute the normalized density map gradient
- move each edge in the gradient direction
- smooth edges using Laplacian filtering (optionally)
- repeat from step 1 with decreasing kernel sizes
Intuitively, the above is equivalent to sharpening the edges' density map. This in turn pulls edges towards the center of their local point spatial distribution, which achieves the bundling.
Implementation
KDEEB is simple to implement and can be easily accelerated using texture splatting for the computation of density maps and their gradients. Our entire implementation is done in C# using OpenGL 1.1.
An implementation of KDEEB will be soon available here.
See also CUBu, our even faster CUDA-based version of KDEEB.
Results
Below are shown several bundling results obtained with KDEEB. The input graphs used are well-known from other Infovis research papers. For comparison purposes, layouts of the same graphs obtained with other recent bundling methods are shown:
- FDEB: Force-directed edge bundling
- WR: Winding roads edge bundling
- MINGLE: Multilevel agglomerative edge bundling
- SBEB: Skeleton-based edge bundling
- KDEEB: Our method
Note: You can download the images below (click, save as..) to see higher-resolution versions.
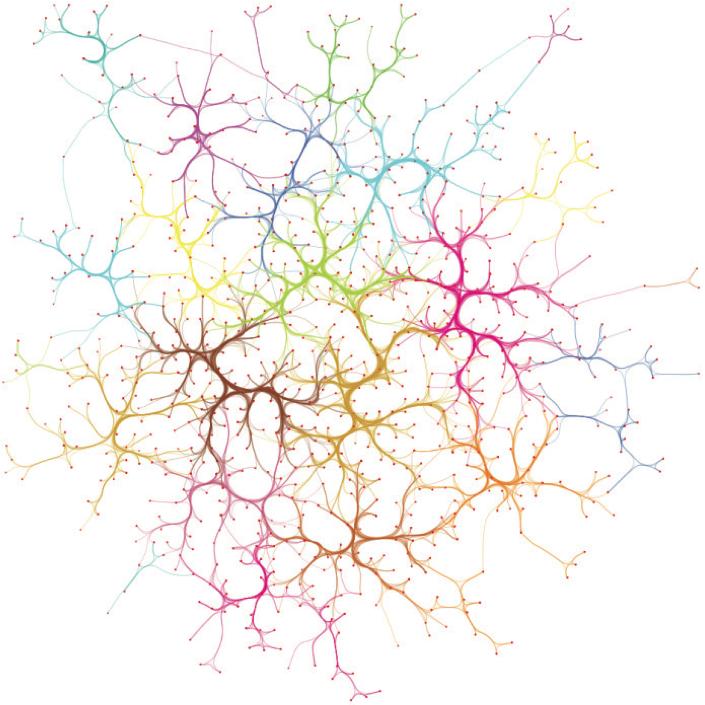

Poker graph (859 nodes, 2127 edges). Left: SBEB. Right: KDEEB
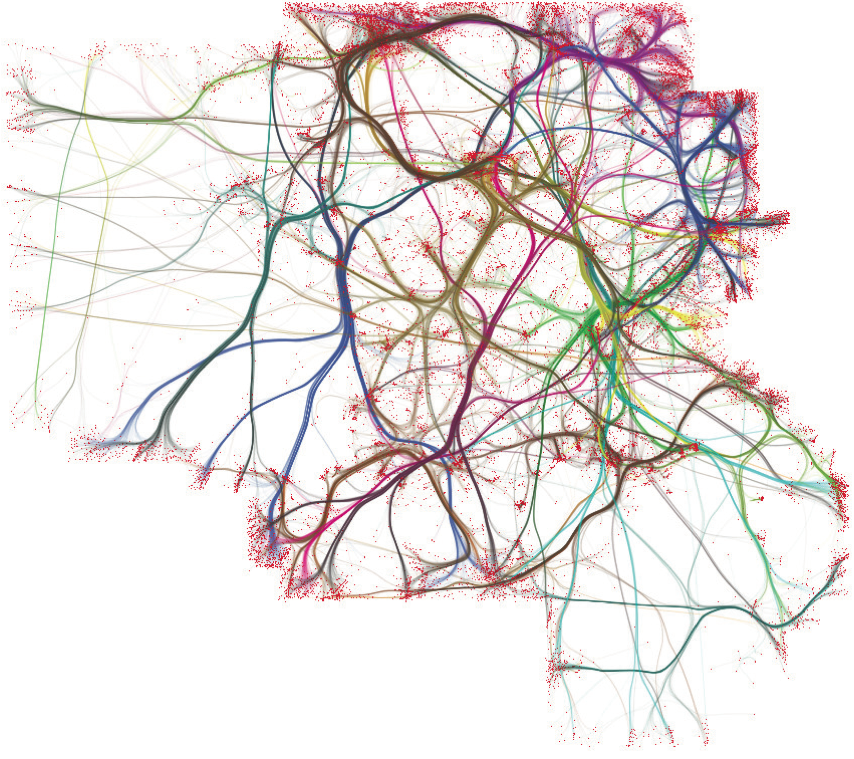
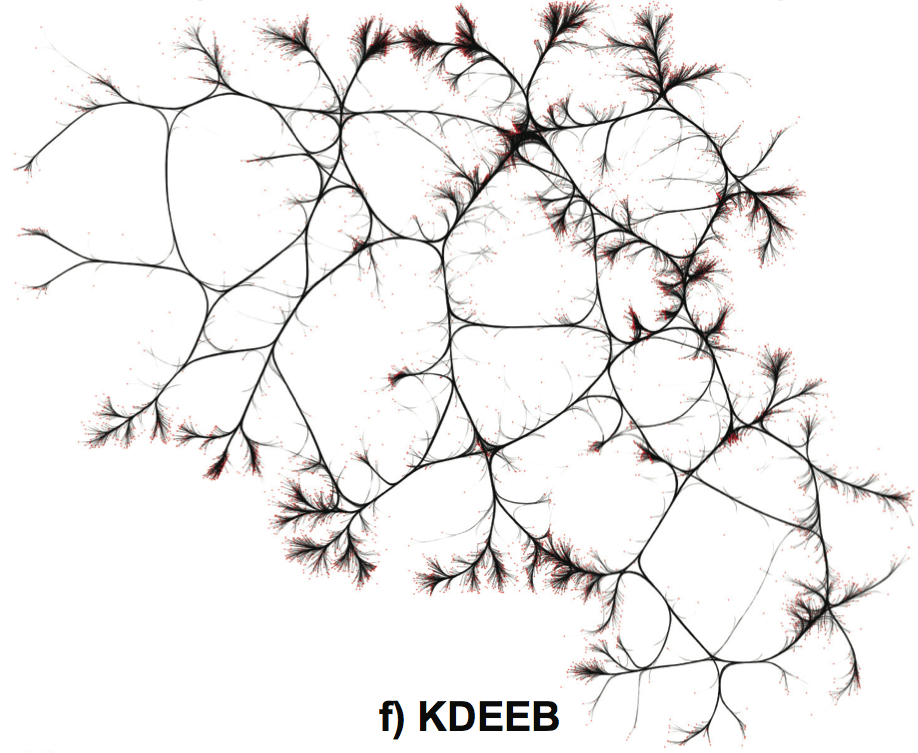
France air-trails graph (34550 nodes, 17275 edges). Left: SBEB. Right: KDEEB

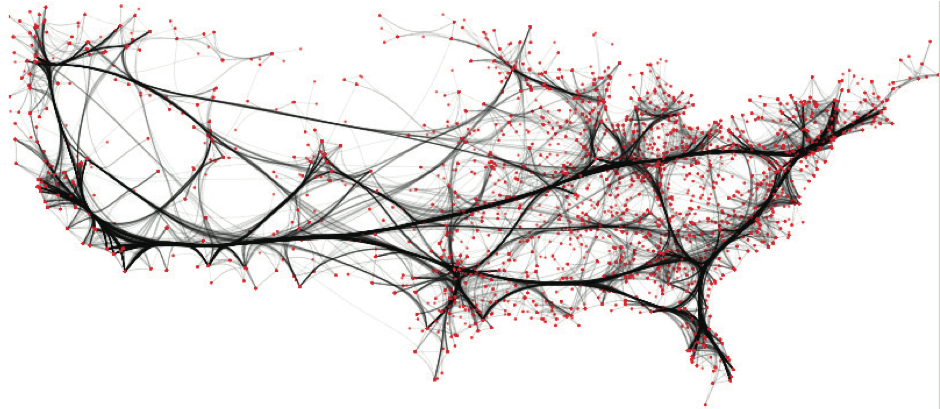
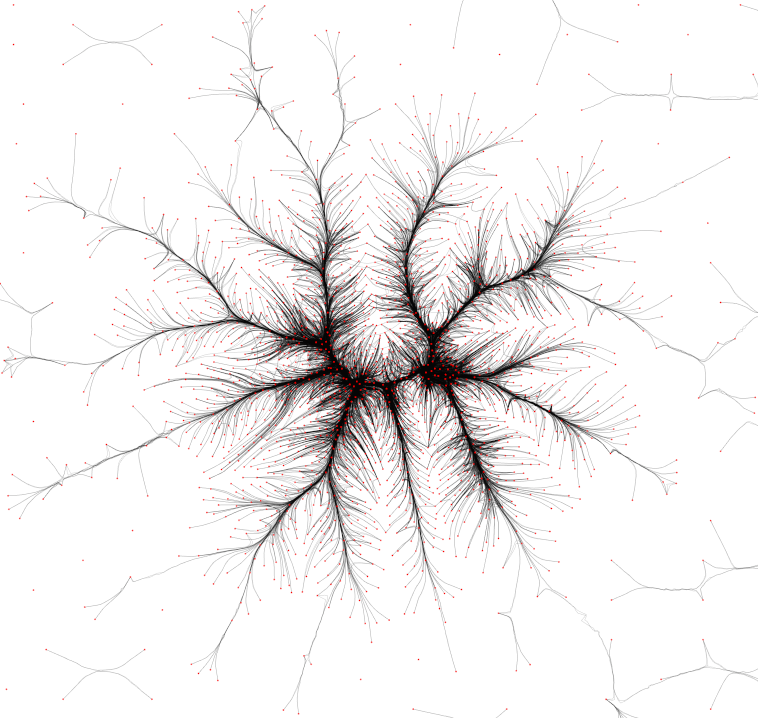
US migrations graph (1715 nodes, 9780 edges). Top-to-bottom: FDEB, WR, KDEEB
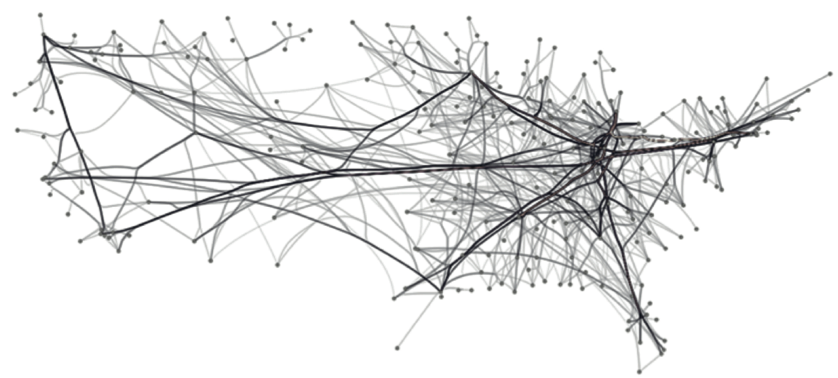
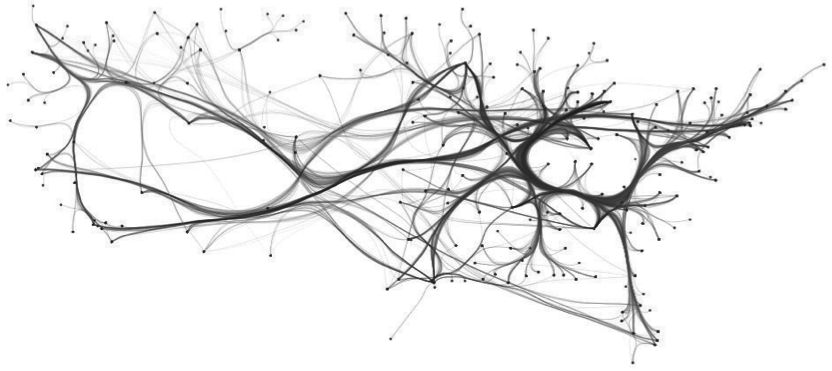
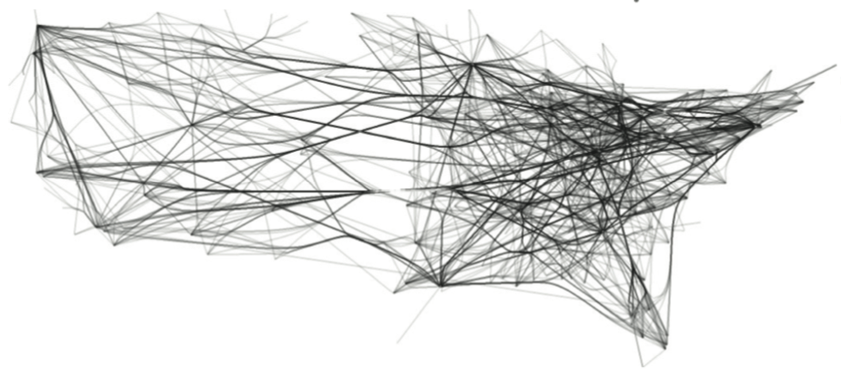
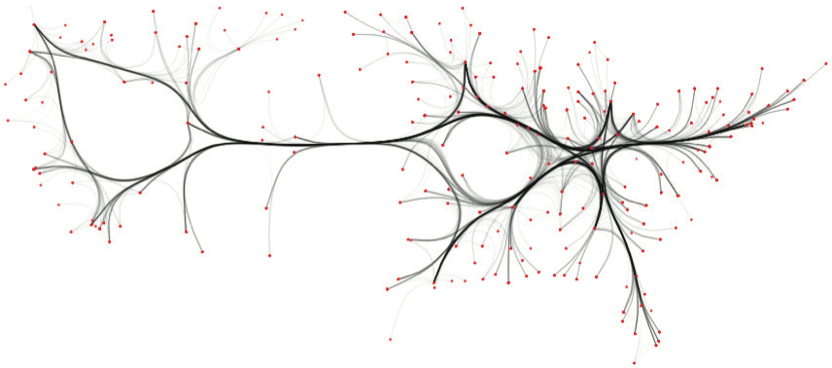
US airlines graph (235 nodes, 2099 edges). Top-to-bottom: FDEB, SBEB, MINGLE, KDEEB

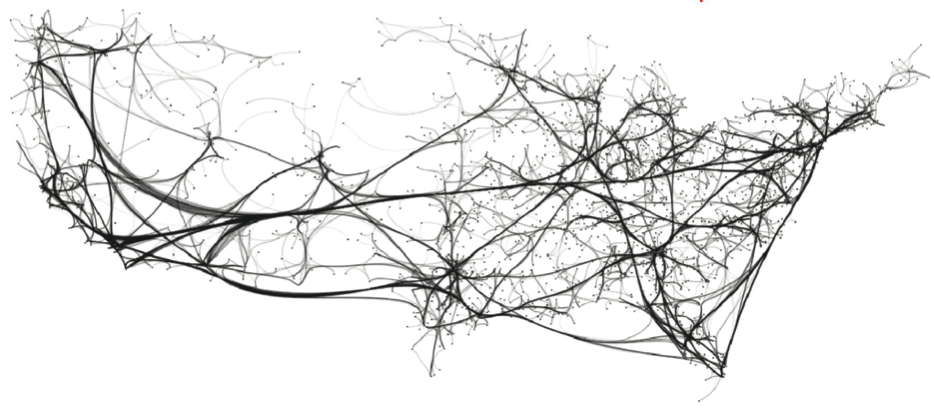
Internet map (2005, Opte project) (23764 edges). Left: LGL. Right: KDEEB

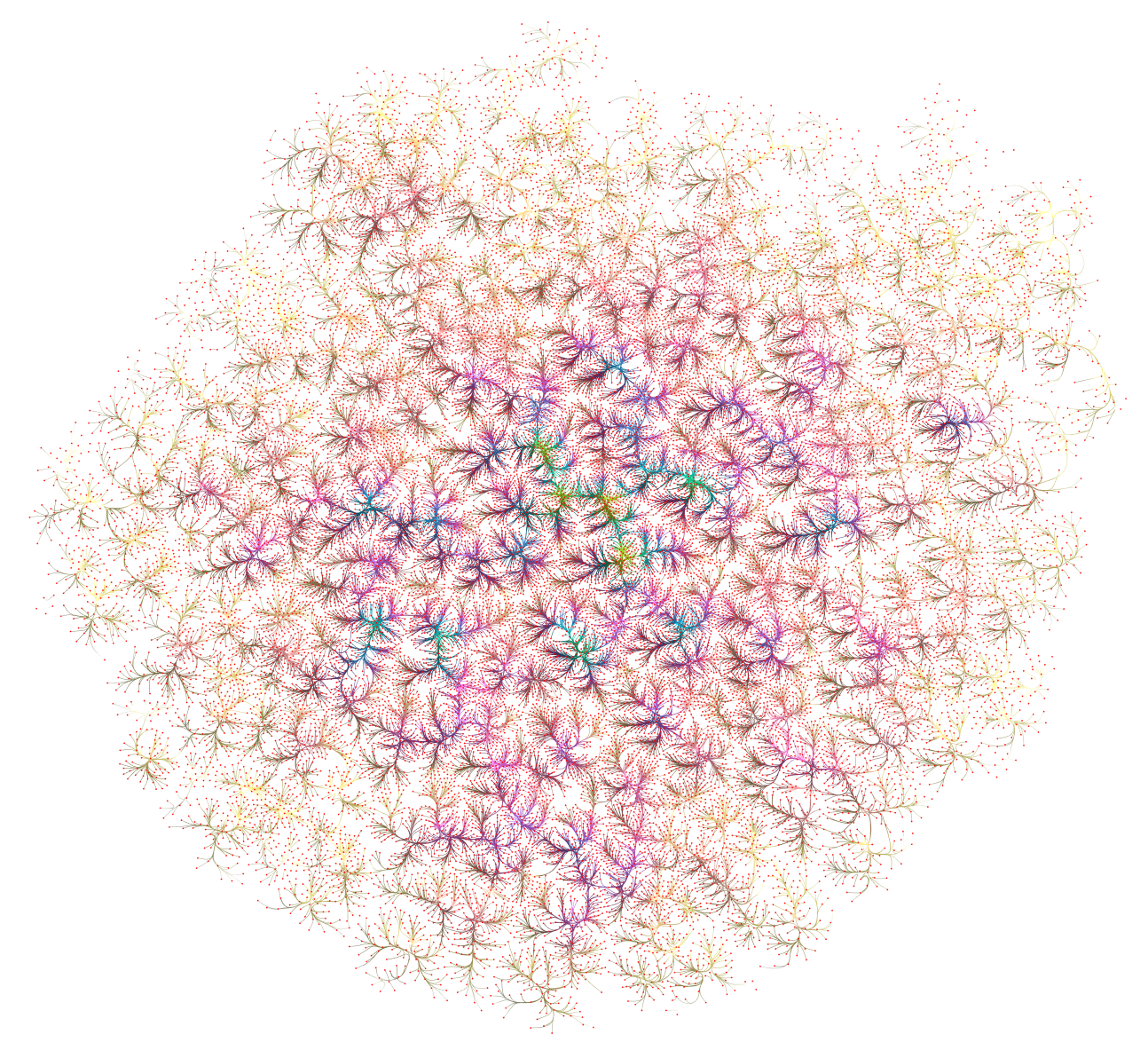
Yeast graph (6646 edges). Left: MINGLE. Right: KDEEB
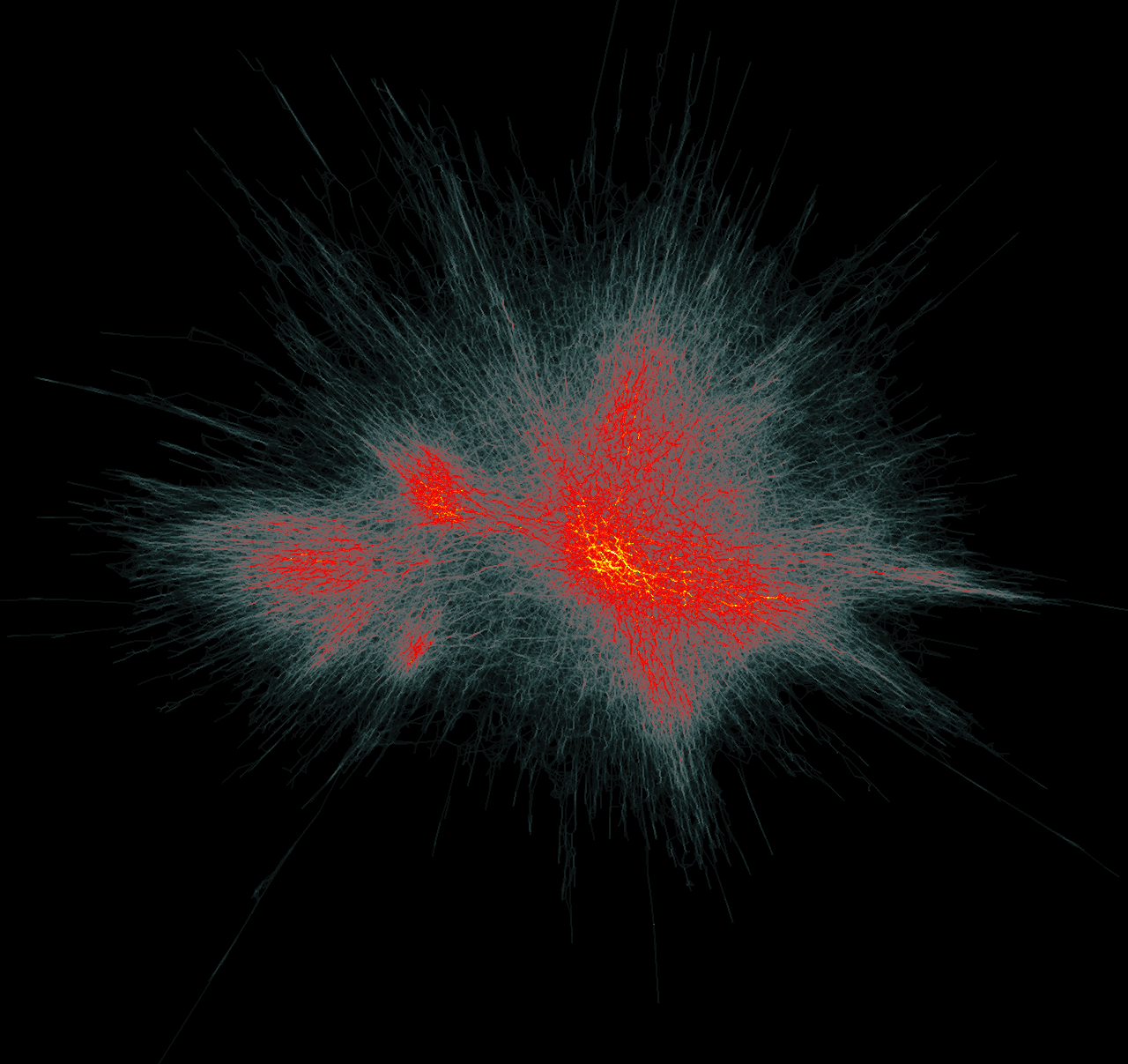

Amazon graph (899792 edges). Left: MINGLE. Right: KDEEB

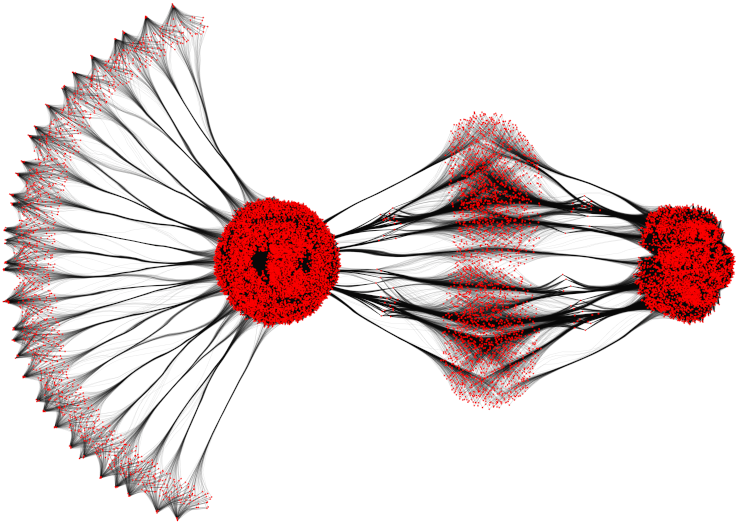
Net-50 graph (464440 edges). Left: MINGLE. Right: KDEEB
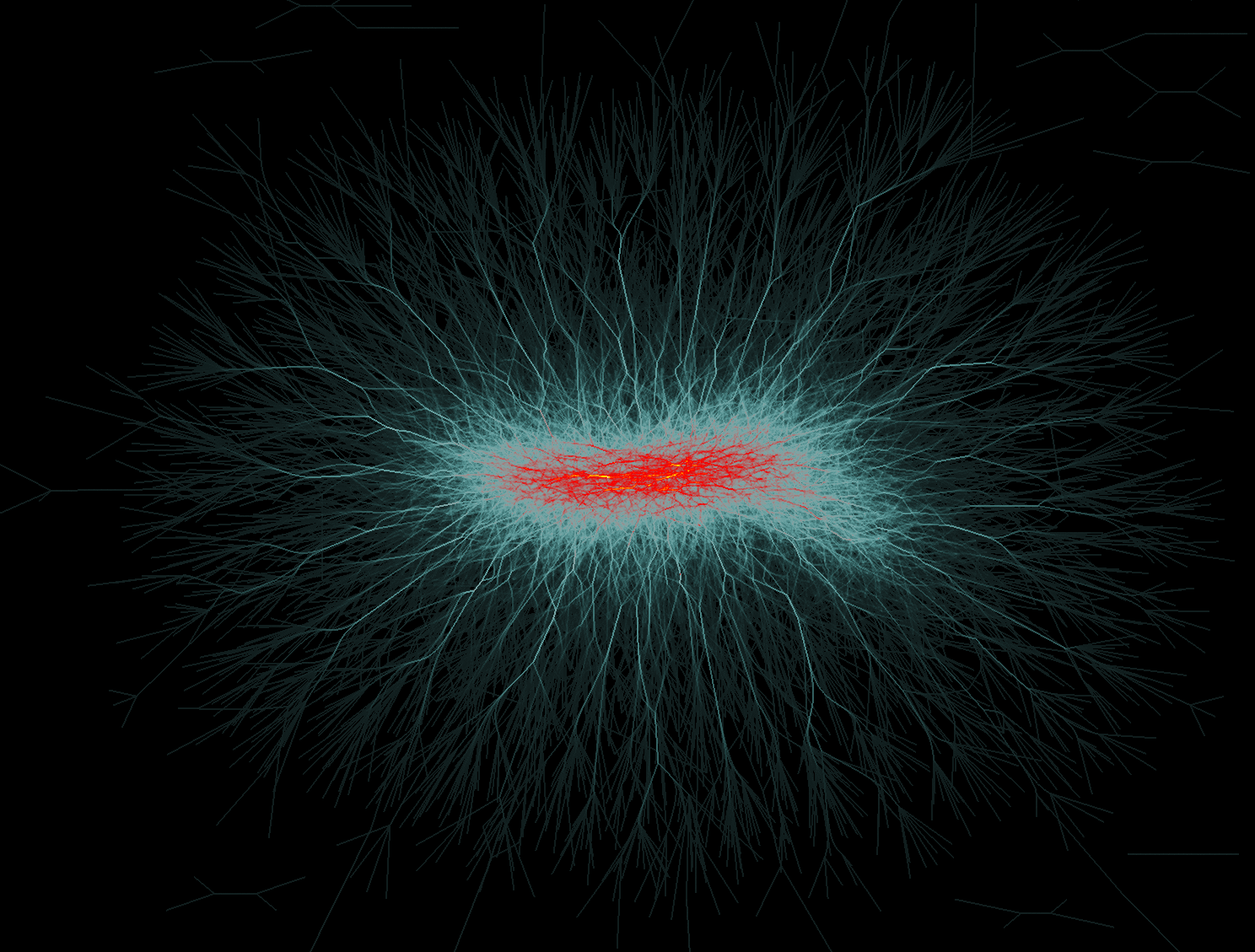
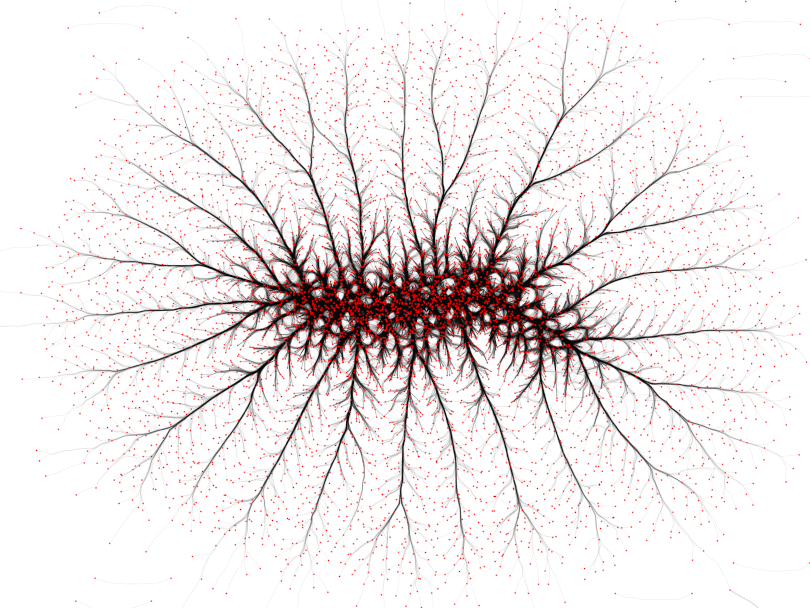
Wiki graph (100762 edges). Left: MINGLE. Right: KDEEB
Publications
This work is described in our Comp. Graph. Forum (EuroVis'12) paper available here.
Acknowledgements
This research was done in collaboration with Christophe Hurter from DGAC/DSNA/DTI, Toulouse, France.
