Shape Processing using PDEs
Shape processing refers to operations such as denoising, fairing, feature extraction, segmentation, simplification, classification, and editing. Such operations are the basic building blocks of many applications in computer graphics, animation, computer vision, and shape retrieval.
Many shape processing operations can be achieved by means of partial differential equations or PDEs. The desired operation is described as a (set of) PDE(s) that act on surface information, such as area, normals, curvature, and similar quantities. PDEs are a very attractive instrument: They allow complex manipulations to be described precisely, compactly, and measurably, and come with efficient and effective numerical methods for solving them.
We present several applications of PDEs in shape processing.
Multiscale segmentation and editing using AMG
Multiscale segmentation refers to the division of a shape's surface in a natural hierarchy of segments. One application is shape editing: Segments represent quasi-flat surface components, separated by ridges. Such a segmentation helps in easy-to-use editing methods, where the user selects a given segment at a desired scale and further manipulates it.
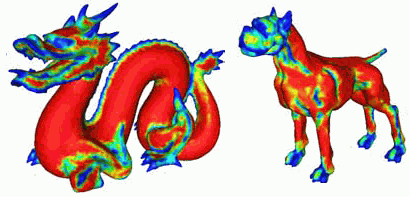
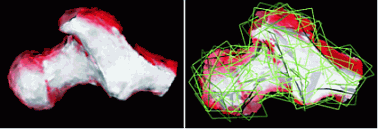
We have implemented a fully automatic multiscale shape segmentation based on the algebraic multigrid technique, or AMG. Local shape flatness is encoded in a stiffness matrix computed on a meshing of the surface. The images below show surface flatness (red=flat, blue=edges) computed on several 3D models.

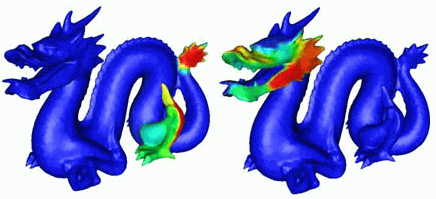
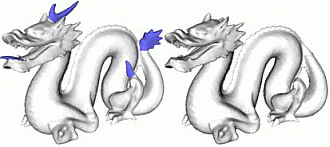
Next, we use the well-known AMG technique to compute a hierarchy of matrices. Each matrix describes the shape at progressively simplified (coarsened) levels, so each matrix entry delivers us an increasingly large shape segment support , whose boundaries fade out into other segment supports as we are approaching a surface crease. The image below shows several such supports on the dragon model. The color changes from red to blue as we evolve on a support towards its borders.
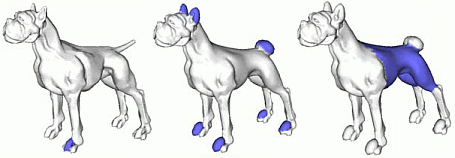
We now compute actual segments as the areas where each segment support has maximal values. This delivers us a surface segmentation. Using different matrices we obtain a multiscale segmentation. The images below show such segmentations for different objects at several scales. The segments follow the natural surface edges present at each scale.
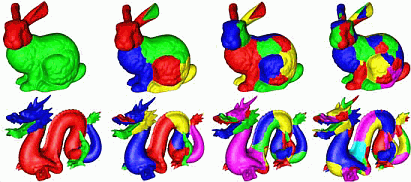
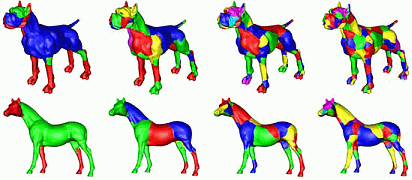
Editing a surface is now easy: We select a desired scale, click on a desired segment, and apply the desired editing. The images below show some sample editing operations applied in this way with just a few mouse clicks. Although these are simple edits, more complex ones can be done equally easily.
PDEs on Point-Based Surfaces
Point based surfaces are a mesh-less popular rendering alternative to triangle meshes, as they store a simple, compact, point cloud instead more memory-consuming, delicate, meshes. The image below shows a 3D model rendered as a point cloud. Points are made small on purpose for illustration aims.

However, many PDE-based surface processing operations can not be directly applied to point clouds since we miss a mesh. We want to add such operations to point cloud editors such as the well-known PointShop.
We demonstrate the applicability of PDE methods to point clouds without the need to construct a global, consistent, mesh. We developed a mathematical framework that moves classical mesh-based PDE operations into a mesh-less setting. The key idea is to use local tangent planes and triangulations to discretize the PDEs and then assemble the results in a global stiffness matrix without the need of a global mesh. Details are provided in this paper.
Curvature estimation
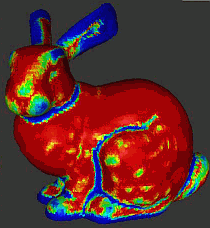
A fundamental tool in surface processing is estimating the curvature of the shape. Several differential operators can be used for this. The image below demonstrates that such operators can be readily applied to mesh-less point clouds. Red colors indicate flat areas, blue indicates curved areas.
Point cloud segmentation
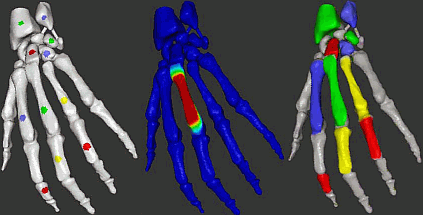
We can use PDEs to segment a point cloud. We place several color markers on a point cloud (first image in the sequence below). Next, we spread the colors using an anisotropic diffusion PDE where the diffusion stops at sharp edges, computed by estimating curvature directly on the point cloud. The second image shows the diffusion signal from one of the markers. At the end, segments separated by edges get filled with the given colors (third image).
Texture generation
Several PDE methods exist for generating natural-looking textures on mesh surfaces. The images below show that these methods can be readily transferred on point clouds using our mathematical framework.
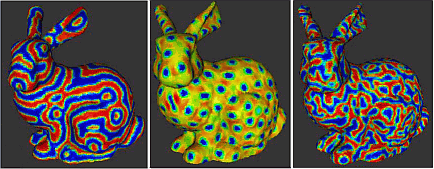
Bump mapping
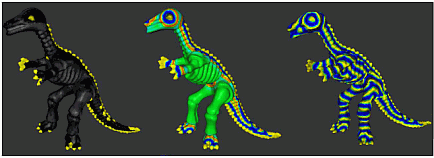
PDEs can also be used to modify the shape of the surface, not just its colors. The image below shows the same PDEs used above to create textures, now used to create a bump mapping appearance, by modifying the normals and positions of the points in the point cloud.
Multiscale rendering of point clouds
Rendering of large point clouds containing hundreds of thousands of points, or more, can be costly. Multiscale methods can accelerate this by rendering the cloud at simplified levels of detail. So far, the main approach was to use larger point primitives, rendered as ellipses, to display groups of close points. However, such primitives cannot approximate well large groups of points so provide only limited simplification.
To address this, we generalized the rendering primitive from an ellipse to a general texture. First, we do a multiscale segmentation of the point cloud using the Algebraic Multigrid (AMG) method earlier described on this page. AMG inherently works mesh-less so is ideally suited for point clouds. Next, we store each quasi-planar segment support into an opacity texture, and render these texture splats on quads aligned on the best approximating planes of their points (computed using principal component analysis). The splats naturally blend at edges creating a simplified mesh-less rendering. For details, see this paper.
The image below shows a point cloud model (left) and the size and orientation of the texture splats (right).
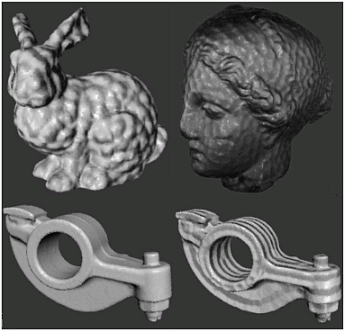
The image below shows several point clouds rendered at full resolution with ellipse primitives (top) and the same models rendered with our simplified texture splats (bottom). The original clouds have 50..180K points while the texture method uses 100..400 splats, each of a few hundred texels on the average.

Although there is some clear loss of detail, the simplification factor is also very high. This makes this method suitable for quick simplified previews or level-of-detail rendering contexts.
Collaboration
Most of the above methods have been developed in collaboration with prof. Martin Rumpf, dr. Tobias Preusser, dr. Ulrich Clarenz, dr. Ulrich Weikard, and dr. Marc-Alexander Schweitzer from the Univ. of Bonn, Germany.
Software
We implemented above methods for PDE-based processing of point clouds in a modified version of the well-known QSplat software rendering tool. Our software is available here for Linux systems.
Publications
See the following papers available here:
- 39 (AMG for surface segmentation)
- 57, 48, 44, 41 (point-based rendering)
